This worked example shows how you can use ANTS Performance Profiler to identify the most time-critical parts of a demonstration application, particularly where two different approaches to a problem are optimal in different circumstances.

Note that the demonstration application used in this worked example is supplied with ANTS Performance Profiler 6.3 and later.

Introducing TimeLineDemo

This worked example uses TimeLineDemo.

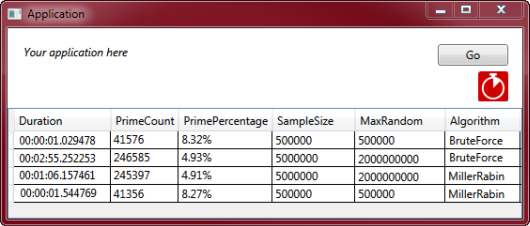
TimeLineDemo is a simple Windows application that checks which of a set of numbers are prime.

There are two different versions of TimeLineDemo:

• In Brute Force configuration, a brute-force method is used to check whether the number is prime.

  The Brute Force build of TimeLineDemo is found in %Program Files%\Red Gate\ANTS Performance Profiler 7\Tutorials\CS\Precompiled\TimeLine\BruteForce\

• In Miller-Rabin configuration, the Miller-Rabin algorithm is used to check whether the number is prime.

  The Miller-Rabin build of TimeLineDemo is found in %Program Files%\Red Gate\ANTS Performance Profiler 7\Tutorials\CS\Precompiled\TimeLine\MillerRabin\

The application has two options:

• Max Random
• Sample Size

When TimeLineDemo first starts, it creates a list of as many prime numbers as possible in 15 seconds.

When you click Go, TimeLineDemo creates a list of positive integers, which is Sample Size items long. All of the integers are random numbers between 1 and Max Random. For each integer in the list, TimeLineDemo checks whether the number is prime, using the following algorithm:

1. If the number is in the list created in the first 15 seconds, it is prime.
2. If a number in the list created in the first 15 seconds is a factor of the current number, the current number is not prime.
3. In all other cases, use either a brute-force mechanism or the Miller-Rabin algorithm to check whether the number is prime (depending on the build in use).

Note: Strictly speaking, the Miller-Rabin algorithm is probabilistic. For the purposes of this demonstration, however, the algorithm can be assumed to be deterministic. This is because the algorithm's results are exact for integers which are smaller than the largest integer that the field accepts.

Walkthrough

Conclusion

This walkthrough has demonstrated a realistic programming scenario. It has compared two methods for testing if a number is prime and shown that Miller-Rabin is more efficient than the brute force approach when the number being tested is large.

This walkthrough has also demonstrated that you can select just a portion of the timeline when analyzing results, allowing you to ignore a slow initialization phase, for example.

Learning more

To perform the task demonstrated in this walkthrough more efficiently, you can use the following additional functionality:

• To help you identify the section of the timeline to select, you can refer to the Event markers in the Events bar.
• You can name and bookmark sections of the timeline.

For more information, see Working with the timeline.